“I’m more frightened than interested by artificial intelligence – in fact, perhaps fright and interest are not far away from one another. Things can become real in your mind, you can be tricked, and you believe things you wouldn’t ordinarily. A world run by automatons doesn’t seem completely unrealistic anymore. It’s a bit chilling.” —Gemma Whelan

什麼是機器學習？

假設我知道今天下雨的機率，但不知道它的權重是多少，換句話說就是，我不知道它跟明天下雨的機率有多大的關聯性，這時候我們就需要使用機器學習，讓機器從過往的資料中，去猜特徵的權重是多少。

機器學習是怎麼去找到函數的呢?

首先我們會先假定一個如圖的藍色函數，那這個函數我們已經知道特徵是什麼，以前面的例子來說，這邊的x就是今天下雨的機率，w是我們不知道的權重，所以先隨便猜一個。

那這個猜出來的函數，效果大概率會非常非常的爛，從圖上可以看到，藍色是過往資料中正確的答案，紫色是帶入這個函數後得到的答案，差蠻多的。

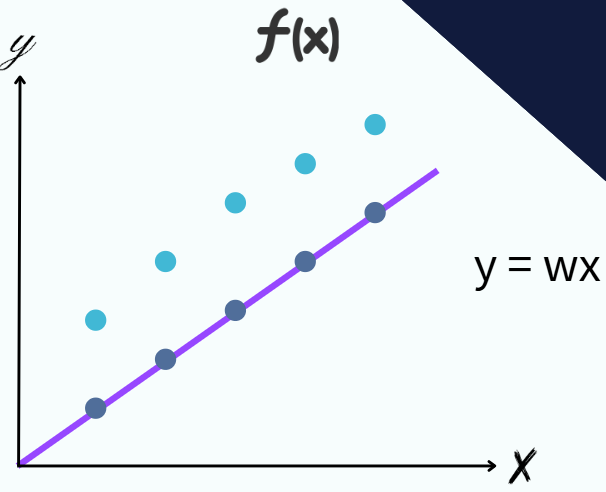
那既然函數很爛，我們就需要調整它的權重，怎麼調整呢？

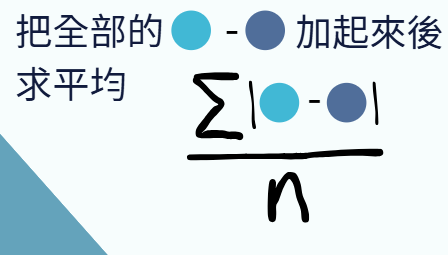
要判斷一個函數是不是夠厲害，其實只要看這個函數對全部的輸入所得到的輸出，是否跟正確答案夠接近，所以我們就定義一個東西叫做Loss，這個Loss會把所有輸入帶入這個函式得到的輸出跟正確答案相減，全部加總起來後取平均。這是Loss的其中一種算法。

這只是我們初始的一個w，它的Loss，如果我們把每個w的Loss都算出來，放到平面座標後，我們可以得到一個x軸是w，y軸是Loss(w)。

理所當然的，我們的目標就是loss最小的那個地方所對應的w，就是我們這個函數應該要選的w。

最直觀的方式就是暴力窮舉法，我們列出每一個w的Loss，選那個最低的，但這種方式可行嗎？

在參數很少的時候是可行的，但是參數一旦變多，窮舉所花的時間會變非常的久。那我們就採用另一種方式。

這種方式叫做gradient descent，它的做法是將最剛開始帶入的w所得到的loss，也就是紅色圈起來的部分，此時我們去算出這個紅點做微分的斜率：

如果它的斜率是正的，那代表它是左下到右上，所以它接下來要往左走，也就是w會變小。

反之斜率如果是負的，那代表它是左上到右下，那就是往右走，w變大。

照這個方法下去，我們可以找到一個地方斜率為0。

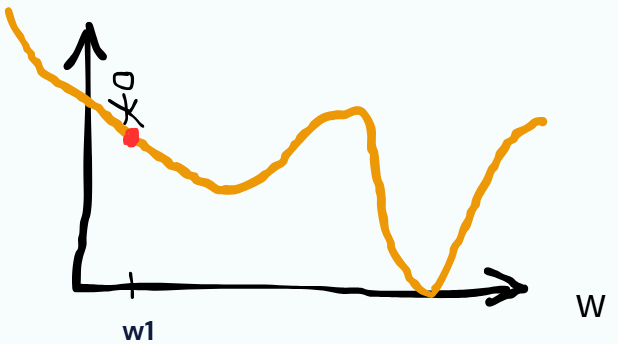
斜率為0可能是全局最小或者是局部最小，至於遇到局部最小怎麼解決，有興趣的可以參考李教授的機器學習系列【機器學習2021】預測本頻道觀看人數 (上) - 機器學習基本概念簡介 (youtube.com)！